Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
Class 10 is an important year in a student’s life and Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 10 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete NCERT Class 10 Maths Book syllabus.

1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Solutions:
Graphical method to find zeroes:-
Total number of zeroes in any polynomial equation = total number of times the curve intersects x-axis.
(i) In the given graph, the number of zeroes of p(x) is 0 because the graph is parallel to x-axis does not cut it at any point.
(ii) In the given graph, the number of zeroes of p(x) is 1 because the graph intersects the x-axis at only one point.
(iii) In the given graph, the number of zeroes of p(x) is 3 because the graph intersects the x-axis at any three points.
(iv) In the given graph, the number of zeroes of p(x) is 2 because the graph intersects the x-axis at two points.
(v) In the given graph, the number of zeroes of p(x) is 4 because the graph intersects the x-axis at four points.
(vi) In the given graph, the number of zeroes of p(x) is 3 because the graph intersects the x-axis at three points.
1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
Solutions:
(i) x2 –2x –8
⇒ x2 – 4x+2x–8 = x(x–4)+2(x–4) = (x-4)(x+2)
Therefore, zeroes of polynomial equation x2 –2x–8 are (4, -2)
Sum of zeroes = 4–2 = 2 = -(-2)/1 = -(Coefficient of x)/(Coefficient of x2 )
Product of zeroes = 4×(-2) = -8 =-(8)/1 = (Constant term)/(Coefficient of x2 )
(ii) 4s2 –4s+1
⇒4s2 –2s–2s+1 = 2s(2s–1)–1(2s-1) = (2s–1)(2s–1)
Therefore, zeroes of polynomial equation 4s2 –4s+1 are (1/2, 1/2)
Sum of zeroes = (½)+(1/2) = 1 = -(-4)/4 = -(Coefficient of s)/(Coefficient of s2 )
Product of zeros = (1/2)×(1/2) = 1/4 = (Constant term)/(Coefficient of s2 )
(iii) 6x2 –3–7x
⇒6x2 –7x–3 = 6x2 – 9x + 2x – 3 = 3x(2x – 3) +1(2x – 3) = (3x+1)(2x-3)
Therefore, zeroes of polynomial equation 6x2 –3–7x are (-1/3, 3/2)
Sum of zeroes = -(1/3)+(3/2) = (7/6) = -(Coefficient of x)/(Coefficient of x2 )
Product of zeroes = -(1/3)×(3/2) = -(3/6) = (Constant term) /(Coefficient of x2 )
(iv) 4u2 +8u
⇒ 4u(u+2)
Therefore, zeroes of polynomial equation 4u2 + 8u are (0, -2).
Sum of zeroes = 0+(-2) = -2 = -(8/4) = = -(Coefficient of u)/(Coefficient of u2 )
Product of zeroes = 0×-2 = 0 = 0/4 = (Constant term)/(Coefficient of u2 )
(v) t2 –15
⇒ t2 = 15 or t = ±√15
Therefore, zeroes of polynomial equation t2 –15 are (√15, -√15)
Sum of zeroes =√15+(-√15) = 0= -(0/1)= -(Coefficient of t) / (Coefficient of t2 )
Product of zeroes = √15×(-√15) = -15 = -15/1 = (Constant term) / (Coefficient of t2 )
(vi) 3x2 –x–4
⇒ 3x2 –4x+3x–4 = x(3x-4)+1(3x-4) = (3x – 4)(x + 1)
Therefore, zeroes of polynomial equation3x2 – x – 4 are (4/3, -1)
Sum of zeroes = (4/3)+(-1) = (1/3)= -(-1/3) = -(Coefficient of x) / (Coefficient of x2 )
Product of zeroes=(4/3)×(-1) = (-4/3) = (Constant term) /(Coefficient of x2 )
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes, respectively.
(i) 1/4 , -1
Solution:
From the formulas of sum and product of zeroes, we know,
Sum of zeroes = α+β
Product of zeroes = α β
Sum of zeroes = α+β = 1/4
Product of zeroes = α β = -1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2 –(α+β)x +αβ = 0
x2 –(1/4)x +(-1) = 0
4x2 –x-4 = 0
Thus, 4x2 –x–4 is the quadratic polynomial.
(ii) √2, 1/3
Solution:
Sum of zeroes = α + β =√2
Product of zeroes = α β = 1/3
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2 –(α+β)x +αβ = 0
x2 –(√2)x + (1/3) = 0
3x2 -3√2x+1 = 0
Thus, 3x2 -3√2x+1 is the quadratic polynomial.
(iii) 0, √5
Solution:
Given,
Sum of zeroes = α+β = 0
Product of zeroes = α β = √5
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly
as:-
x2 –(α+β)x +αβ = 0
x2 –(0)x +√5= 0
Thus, x2 +√5 is the quadratic polynomial.
(iv) 1, 1
Solution:
Given,
Sum of zeroes = α+β = 1
Product of zeroes = α β = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2 –(α+β)x +αβ = 0
x2 –x+1 = 0
Thus, x2 –x+1 is the quadratic polynomial.
(v) -1/4, 1/4
Solution:
Given,
Sum of zeroes = α+β = -1/4
Product of zeroes = α β = 1/4
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2 –(α+β)x +αβ = 0
x2 –(-1/4)x +(1/4) = 0
4x2 +x+1 = 0
Thus, 4x2 +x+1 is the quadratic polynomial.
(vi) 4, 1
Solution:
Given,
Sum of zeroes = α+β =4
Product of zeroes = αβ = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written directly as:-
x2 –(α+β)x+αβ = 0
x2 –4x+1 = 0
Thus, x2 –4x+1 is the quadratic polynomial.
1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 -3x2 +5x–3 , g(x) = x2 –2
Solution:
Given,
Dividend = p(x) = x3 -3x2 +5x–3
Divisor = g(x) = x2 – 2
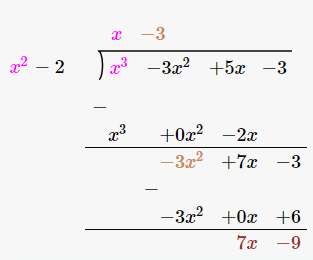
Therefore, upon division we get,
Quotient = x–3
Remainder = 7x–9
(ii) p(x) = x4 -3x2 +4x+5 , g(x) = x2 +1-x
Solution:
Given,
Dividend = p(x) = x4 – 3x2 + 4x +5
Divisor = g(x) = x2 +1-x
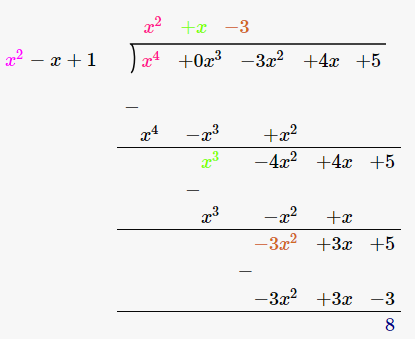
Therefore, upon division we get,
Quotient = x2 + x–3
Remainder = 8
(iii) p(x) =x4 –5x+6, g(x) = 2–x2
Solution:
Given,
Dividend = p(x) =x4 – 5x + 6 = x4 +0x2 –5x+6
Divisor = g(x) = 2–x2 = –x2 +2
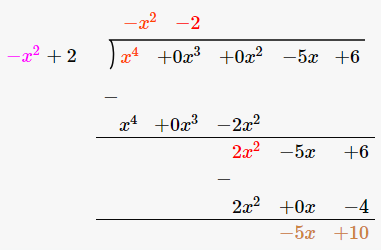
Therefore, upon division we get,
Quotient = -x2 -2
Remainder = -5x + 10
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2 -3, 2t4 +3t3 -2t2 -9t-12
Solutions:
Given,
First polynomial = t2 -3
Second polynomial = 2t4 +3t3 -2t2 -9t-12
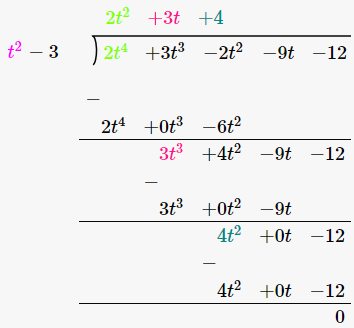
As we can see, the remainder is left as 0. Therefore, we say that, t2 -3 is a factor of 2t4 +3t3 -2t2 -9t-12.
(ii)x2 +3x+1 , 3x4 +5x3 -7x2 +2x+2
Solutions:
Given,
First polynomial = x2 +3x+1
Second polynomial = 3x4 +5x3 -7x2 +2x+2
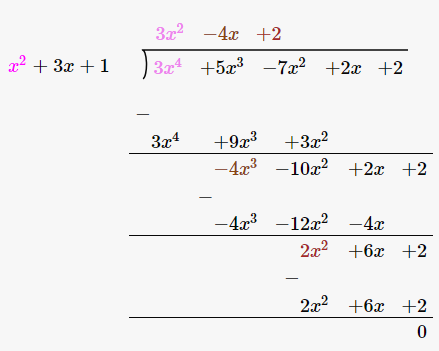
As we can see, the remainder is left as 0. Therefore, we say that, x2 + 3x + 1 is a factor of 3x4 +5x3 -7x2 +2x+2.
(iii) x3 -3x+1, x5 -4x3 +x2 +3x+1
Solutions:
Given,
First polynomial = x3 -3x+1
Second polynomial = x5 -4x3 +x2 +3x+1
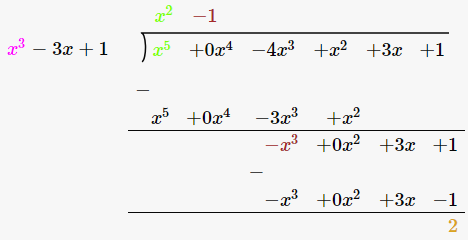
As we can see, the remainder is not equal to 0. Therefore, we say that, x3 -3x+1 is not a factor of x5 -4x3 +x2 +3x+1 .
3. Obtain all other zeroes of 3x4 +6x3 -2x2 -10x-5, if two of its zeroes are √(5/3) and – √(5/3).
Solutions:
Since this is a polynomial equation of degree 4, hence there will be total 4 roots.
√(5/3) and – √(5/3) are zeroes of polynomial f(x).
∴ (x –√(5/3) ) (x+√(5/3) = x2 -(5/3) = 0
(3x2 −5)=0, is a factor of given polynomial f(x).
Now, when we will divide f(x) by (3x2 −5) the quotient obtained will also be a factor of f(x) and the remainder will be 0.

Therefore, 3x4 +6x3 −2x2 −10x–5 = (3x2 –5) (x2 +2x+1)
Now, on further factorizing (x2 +2x+1) we get,
x2 +2x+1 = x2 +x+x+1 = 0
x(x+1)+1(x+1) = 0
(x+1)(x+1) = 0
So, its zeroes are given by: x= −1 andx = −1.
Therefore, all four zeroes of given polynomial equation are:
√(5/3),- √(5/3) , −1 and −1.
Hence, is the answer.
4. On dividing x3 -3x2 +x+2 by a polynomial g(x), the quotient and remainder were x–2 and –2x+4, respectively. Find g(x).
Solution:
Given,
Dividend, p(x) = x3 -3x2 +x+2
Quotient = x-2
Remainder = –2x+4
We have to find the value of Divisor, g(x) =?
As we know,
Dividend = Divisor × Quotient + Remainder
∴ x3 -3x2 +x+2 = g(x)×(x-2) + (-2x+4)
x3 -3x2 +x+2-(-2x+4) = g(x)×(x-2)
Therefore, g(x) × (x-2) = x3 -3x2 +3x-2
Now, for finding g(x) we will divide x3 -3x2 +3x-2 with (x-2)
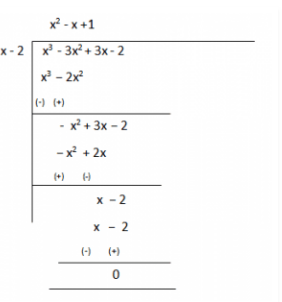
Therefore, g(x) = (x2 –x+1)
5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solutions:
According to the division algorithm, dividend p(x) and divisor g(x) are two polynomials, where g(x)≠0. Then we can find the value of quotient q(x) and remainder r(x), with the help of below given formula;
Dividend = Divisor × Quotient + Remainder
∴ p(x) = g(x)×q(x)+r(x)
Where r(x) = 0 or degree of r(x)<degree of g(x).
Now let us proof the three given cases as per division algorithm by taking examples for each.
(i) deg p(x) = deg q(x)
Degree of dividend is equal to degree of quotient, only when the divisor is a constant term.
Let us take an example, p(x) = 3x2 +3x+3 is a polynomial to be divided by g(x) = 3.
So, (3x2 +3x+3)/3 = x2 +x+1 = q(x)
Thus, you can see, the degree of quotient q(x) = 2, which also equal to the degree of dividend p(x).
Hence, division algorithm is satisfied here.
(ii) deg q(x) = deg r(x)
Let us take an example, p(x) = x2 + 3 is a polynomial to be divided by g(x) = x – 1.
So, x2 + 3 = (x – 1)×(x) + (x + 3)
Hence, quotient q(x) = x
Also, remainder r(x) = x + 3
Thus, you can see, the degree of quotient q(x) = 1, which is also equal to the degree of remainder r(x).
Hence, division algorithm is satisfied here.
(iii) deg r(x) = 0
The degree of remainder is 0 only when the remainder left after division algorithm is constant.
Let us take an example, p(x) = x2 + 1 is a polynomial to be divided by g(x) = x.
So, x2 + 1 = (x)×(x) + 1
Hence, quotient q(x) = x
And, remainder r(x) = 1
Clearly, the degree of remainder here is 0.
Hence, division algorithm is satisfied here.
1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 +x2 -5x+2; -1/2, 1, -2
Solution:
Given, p(x) = 2x3 +x2 -5x+2
And zeroes for p(x) are = 1/2, 1, -2
∴ p(1/2) = 2(1/2)3 +(1/2)2 -5(1/2)+2 = (1/4)+(1/4)-(5/2)+2 = 0
p(1) = 2(1)3 +(1)2 -5(1)+2 = 0
p(-2) = 2(-2)3 +(-2)2 -5(-2)+2 = 0
Hence, proved 1/2, 1, -2 are the zeroes of 2x3 +x2 -5x+2.
Now, comparing the given polynomial with general expression, we get;
∴ ax3 +bx2 +cx+d = 2x3 +x2 -5x+2
a=2, b=1, c= -5 and d = 2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3 +bx2 +cx+d , then;
α +β+γ = –b/a
αβ+βγ+γα = c/a
α βγ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α+β+γ = ½+1+(-2) = -1/2 = –b/a
αβ+βγ+γα = (1/2×1)+(1 ×-2)+(-2×1/2) = -5/2 = c/a
α β γ = ½×1×(-2) = -2/2 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
(ii) x3 -4x2 +5x-2 ;2, 1, 1
Solution:
Given, p(x) = x3 -4x2 +5x-2
And zeroes for p(x) are 2,1,1.
∴ p(2)= 23 -4(2)2 +5(2)-2 = 0
p(1) = 13 -(4×12 )+(5×1)-2 = 0
Hence proved, 2, 1, 1 are the zeroes of x3 -4x2 +5x-2
Now, comparing the given polynomial with general expression, we get;
∴ ax3 +bx2 +cx+d = x3 -4x2 +5x-2
a = 1, b = -4, c = 5 and d = -2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3 +bx2 +cx+d , then;
α + β + γ = –b/a
αβ + βγ + γα = c/a
α β γ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α +β+γ = 2+1+1 = 4 = -(-4)/1 = –b/a
αβ+βγ+γα = 2×1+1×1+1×2 = 5 = 5/1= c/a
αβγ = 2×1×1 = 2 = -(-2)/1 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.
Solution:
Let us consider the cubic polynomial is ax3 +bx2 +cx+d and the values of the zeroes of the polynomials be α, β, γ.
As per the given question,
α+β+γ = -b/a = 2/1
αβ +βγ+γα = c/a = -7/1
α βγ = -d/a = -14/1
Thus, from above three expressions we get the values of coefficient of polynomial.
a = 1, b = -2, c = -7, d = 14
Hence, the cubic polynomial is x3 -2x2 -7x+14
3. If the zeroes of the polynomial x3 -3x2 +x+1 are a – b, a, a + b, find a and b.
Solution:
We are given with the polynomial here,
p(x) = x3 -3x2 +x+1
And zeroes are given as a – b, a, a + b
Now, comparing the given polynomial with general expression, we get;
∴px3 +qx2 +rx+s = x3 -3x2 +x+1
p = 1, q = -3, r = 1 and s = 1
Sum of zeroes = a – b + a + a + b
-q/p = 3a
Putting the values q and p.
-(-3)/1 = 3a
a=1
Thus, the zeroes are 1-b, 1, 1+b.
Now, product of zeroes = 1(1-b)(1+b)
-s/p = 1-b2
-1/1 = 1-b2
b2 = 1+1 = 2
b = ±√2
Hence,1-√2, 1 ,1+√2 are the zeroes of x3 -3x2 +x+1.
4. If two zeroes of the polynomial x4 -6x3 -26x2 +138x-35 are 2 ± √3, find other zeroes.
Solution:
Since this is a polynomial equation of degree 4, hence there will be total 4 roots.
Let f(x) = x4 -6x3 -26x2 +138x-35
Since 2 +√3 and 2-√3 are zeroes of given polynomial f(x).
∴ [x−(2+√3 )] [x−(2-√3) ] = 0
(x−2−√3 )(x−2+√3 ) = 0
On multiplying the above equation we get,
x2 -4x+1, this is a factor of a given polynomial f(x).
Now, if we will divide f(x) by g(x), the quotient will also be a factor of f(x) and the remainder will be 0.

So, x4 -6x3 -26x2 +138x-35 = (x2 -4x+1)(x2 –2x−35)
Now, on further factorizing (x2 –2x−35) we get,
x2 –(7−5)x −35 = x2 – 7x+5x+35 = 0
x(x −7)+5(x−7) = 0
(x+5)(x−7) = 0
So, its zeroes are given by:
x= −5 and x = 7.
Therefore, all four zeroes of given polynomial equation are: 2+√3 , 2-√3 , −5 and 7.
Q.5: If the polynomial x 4 – 6x 3 + 16x 2 – 25x + 10 is divided by another polynomial x 2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
Let’s divide x 4 – 6x 3 + 16x 2 – 25x + 10 by x 2 – 2x + k.

Given that the remainder of the polynomial division is x + a.
(4k – 25 + 16 – 2k)x + [10 – k(8 – k)] = x + a
(2k – 9)x + (10 – 8k + k 2 ) = x + a
Comparing the coefficients of the above equation, we get;
2k – 9 = 1
2k = 9 + 1 = 10
k = 10/2 = 5
And
10 – 8k + k 2 = a
10 – 8(5) + (5) 2 = a [since k = 5]
10 – 40 + 25 = a
a = -5
Therefore, k = 5 and a = -5.