Home Revise | Maharashtra State Board Class 9 Maths 2 Solutions Chapter 8 Trigonometry

Maharashtra State Board Class 9 Maths 2 Chapter 8 Trigonometry

The Class 9 is an important year in a student’s life and Maharashtra State Board Maths 2 is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 9 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 9 Maths 2 Book syllabus.

NCERT Solutions for Class 10 Science CBSE

Access answers to Maths MSBSHSE Solutions For Class 9 Part 2 Chapter 8 Trigonometry

Practice Set 8.1 Page 104

1.In the Fig.8.12, R is the right angle of PQR. Write the following ratios.

(i) sin P (ii) cos Q (iii) tan P (iv) tan Q

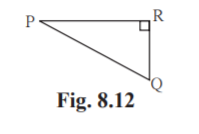
Solution:

(i) sin P = Opposite side of P / Hypotenuse = QR/PQ

(ii) cos Q = Adjacent side of Q / Hypotenuse = QR/PQ

(iii) tan P = Opposite side of P / Adjacent side of P = QR/PR

(iii) tan Q = Opposite side of Q / Adjacent side of Q = PR/QR

2. In the right angled XYZ, XYZ = 90° and a,b,c are the lengths of the sides as shown in the figure. Write the following ratios,

(i) sin X (ii) tan Z (iii) cos X (iv) tan X.

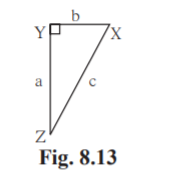
Solution:

(i) sin X = Opposite side of X / Hypotenuse = a/c

(ii) tan Z = Opposite side of Z / Adjacent side of Z = b/a

(iii) cos X = Adjacent side of X / Hypotenuse = b/c

(iv) tan X = Opposite side of X / Adjacent side of X = a/b

3.In right angled LMN, LMN = 90° L = 50° and N = 40°, write the following ratios.

(i) sin 50° (ii) cos 50° (iii) tan 40° (iv) cos 40°

Maharashtra Board Sol Class 9 Maths p2 chapter 8-3

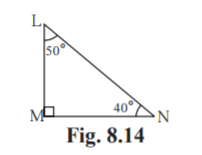
Solution:

(i) sin 50˚ = Opposite side of 50˚ / Hypotenuse = MN/LN

(ii) cos 50˚ = Adjacent side of 50˚ / Hypotenuse = LM/LN

(iii) tan 40˚ = Opposite side of 40˚ / Adjacent side of 40˚ = LM/MN

(iv) cos 40˚ = Adjacent side of 40˚ / Hypotenuse = MN/LN

4.In the figure 8.15,.PQR = 90°, PQS = 90°, PRQ = and QPS =

Write the following trigonometric ratios.

(i) sin , cos , tan

(ii) sin , cos , tan

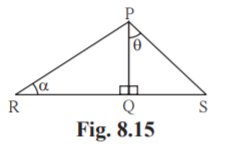
Solution:

(i) sin = Opposite side of /Hypotenuse = PQ/PR

cos = Adjacent side of / Hypotenuse = QR/PR

tan = Opposite side of / Adjacent side of = PQ/QR

(ii) sin = Opposite side of /Hypotenuse = QS/PS

cos = Adjacent side of / Hypotenuse = PQ/PS

tan = Opposite side of / Adjacent side of = QS/PQ

Practice Set 8.2 Page 112

1. In the following table, a ratio is given in each column. Find the remaining two ratios in the column and complete the table.

Solution:

(1) cos = 35/37

sin² +cos² = 1

sin² +(35/37)² = 1

sin² = 1-(35/37)²

sin² = 1-(1225/1369)

sin² = (1369-1225)/1369

sin² = 144/1369

Taking square root on both sides

sin = 12/37

tan = sin /cos

tan = (12/37)÷(35/37)

tan = (12/37)×(37/35) = 12/35

(2) sin =11/61

sin² +cos² = 1

(11/61)² +cos² = 1

cos² = 1-(11/61)²

cos² = 1-(121/3721)

cos² = (3721-121)/3721

cos² = 3600/3721

Taking square root on both sides

cos = 60/61

tan = sin /cos

tan = (11/61)÷(60/61)

tan = (11/61)×(61/60) = 11/60

3. tan = 1

sin /cos = 1

Let sin = cos = k

sin² +cos² = 1

k² +k² = 1

2k² = 1

k² = 1/2

k = 1/√2

sin = k = 1/√2

cos = k = 1/√2

4. sin = 1/2

sin² +cos² = 1

(1/2)² +cos² = 1

cos² = 1-(1/2)²

cos² = 1-(1/4)

cos² = (4-1)/4

cos² = 3/4

Taking square root on both sides

cos = √3/2

tan = sin /cos

tan = (1/2)÷( √3/2)

tan = (1/2)×(2/√3) = 1/√3

(5) cos = 1/√3

sin² +cos² = 1

sin² +(1/√3)² = 1

sin² = 1-(1/√3)²

sin² = 1-(1/3)

sin² = (3-1)/3

sin² = 2/3

Taking square root on both sides

sin = √2/√3

tan = sin /cos

tan = (√2/√3)÷( 1/√3)

tan = (√2/√3)×( 3/1) = √2

(6) tan = 21/20

sin /cos = 21/20

Let sin = 21k

cos = 20k

sin² +cos² = 1

(21k)² +(20k)² = 1

441k² +400k² = 1

841k² = 1

k² = 1/841

Taking square root on both sides

k = 1/29

sin = 21k = 21×(1/29) = 21/29

cos = 20k = 20×(1/29) = 20/29

(7) tan = 8/15

sin /cos = 8/15

Let sin = 8k

cos = 15k

sin² +cos² = 1

(8k)² +(15k)² = 1

64k² +225k² = 1

289k² = 1

k² = 1/289

Taking square root on both sides

k = 1/17

sin = 8k = 8×(1/17) = 8/17

cos = 15k

cos = 15×(1/17)

cos = 15/17

(8) sin = 3/5

sin² +cos² = 1

(3/5)² +cos² = 1

cos² = 1-(3/5)²

cos² = 1-(9/25)

cos² = (25-9)/25

cos² = 16/25

Taking square root on both sides

cos = 4/5

tan = sin /cos

tan = (3/5)÷(4/5)

tan = (3/5)×(5/4)

tan = 3/4

(9) tan = 1/2√2

sin /cos = 1/2√2

Let sin = k

cos = 2√2k

sin² +cos² = 1

(k)² +(2√2k)² = 1

k² +8k² = 1

9k² = 1

k² = 1/9

Taking square root on both sides

k = 1/3

sin = k = 1/3

cos = 2√2k

cos = 2√2×(1/3)

cos = 2√2/3

The completed table is given below.

Sl.No	1	2	3	4	5	6	7	8	9
sin	12/37	11/61	1/√2	1/2	√2/√3	21/29	8/17	3/5	1/3
cos	35/37	60/61	1/√2	√3/2	1/√3	20/29	15/17	4/5	2√2/3
tan	12/35	11/60	1	1/√3	√2	21/20	8/15	3/4	1/2√2

2. Find the values of –

(i) 5 sin 30˚+3tan 45˚

(ii) 4/5 tan² 60˚+3 sin² 60

(iii) 2 sin 30 °+ cos 0˚+ 3 sin 90°

(iv) tan 60/ (sin 60+cos 60 )

(v) cos² 45˚ + sin² 30˚

(vi) cos 60°× cos 30° + sin 60°× sin 30°

Solution:

(i) sin 30˚ = 1/2

tan 45˚ = 1

5 sin 30˚+3tan 45˚ = (5×1/2) +(3×1)

= 5/2 +3

= (5+6)/3

= 11/3

Hence, 5 sin 30˚+3tan 45˚ = 11/3

(ii) tan 60˚ = √3

sin 60˚ = √3/2

4/5 tan² 60˚+3 sin² 60 = (4/5)×√3² + 3×(√3/2)²

= (12/5)+(9/4)

= (48+45)/20

= 93/20

Hence, 4/5 tan² 60˚+3 sin² 60 = 93/20

(iii) sin 30˚ = 1/2

cos 0˚ = 1

sin 90˚ = 1

2 sin 30°+cos 0˚+3 sin 90° = 2×(1/2)+1+3×1

= 1+1+3

= 5

Hence, 2 sin 30°+cos 0˚+3 sin 90° = 5

(iv) tan 60 = √3

sin 60 = √3/2

cos 60 = 1/2

tan 60/ (sin 60+cos 60) = √3 ÷[(√3/2)+( 1/2)]

= √3 ÷[(√3+1)/2]

= √3×2/(√3+1)

= 2√3/(√3+1)

Hence tan 60/ (sin 60+cos 60) = 2√3/(√3+1)

(v) cos 45˚ = 1/√2

sin 30˚ = ½

cos² 45˚ + sin² 30˚ =( 1/√2)² +(1/2)²

= (½)+(1/4)

= 3/4

Hence, cos² 45˚ + sin² 30˚ = 3/4

(vi) cos 60° = 1/2

cos 30° = √3/2

sin 60° = √3/2

sin 30° = 1/2

cos 60°× cos 30° + sin 60°× sin 30° =( ½)×(√3/2)+(√3/2)×(1/2)

= (√3/4)+ (√3/4)

= 2√3/4

= √3/2

Hence, cos 60°× cos 30° + sin 60°× sin 30° = √3/2

3. If sin = 4/5 then find cos.

Solution:

sin = 4/5

sin² +cos² = 1

(4/5)² + cos² = 1

cos² = 1-(4/5)²

cos² = 1-(16/25)

cos² = (25-16)/25

cos² = 9/25

Taking square root on both sides

cos = 3/5

Hence, cos is 3/5

4. If cos = 15/17 then find sin

Solution:

cos = 15/17

sin² +cos² = 1

sin² + (15/17)² = 1

sin² = 1-(15/17)²

sin² = 1-(225/289)

sin² = (289-225)/289

sin² = 64/289

Taking square root on both sides

sin = 8/17

Hence, sin is 8/17

Problem Set 8-Page 113

1. Choose the correct alternative answer for following multiple choice questions.

(i) Which of the following statements is true ?

(A) sin = cos (90-) (B) cos = tan (90-)

(C) sin = tan (90-) (D) tan = tan (90-)

(ii) Which of the following is the value of sin 90° ?

(A)√ 3/2 (B) 0 (C) 1/2 (D) 1

(iii) 2 tan 45° + cos 45° –sin 45° = ?

(A) 0 (B) 1 (C) 2 (D) 3

(iv) cos 28° /sin 62° = ?

(A) 2 (B) -1 (C) 0 (D) 1

Solution:

(i) sin = cos (90-)

Hence, Option A is the answer.

(ii) sin 90˚ = 1

Hence, Option D is the answer.

(iii) tan 45° = 1

cos 45° = 1/√2

sin 45° = 1/√2

2 tan 45° + cos 45° –sin 45° = (2×1)+(1/√2)-(1/√2) = 2

Hence Option C is the answer.

(iv) cos 28° = sin (90-28) = sin 62˚

cos 28°/sin 62 ° = sin 62˚/ sin 62˚ = 1

Hence Option D is the answer.

2. In right angled TSU, TS = 5, S = 90°, SU = 12 then find sin T, cos T, tan T. Similarly find sin U, cos U, tan U.

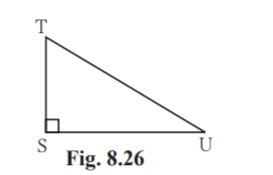
Solution:

Given TS = 5

SU = 12

S = 90˚

TU² = TS² +SU² [Pythagoras theorem]

TU² = 5² +12²

TU² = 25+144

TU² = 169

Taking square root on both sides

TU = 13

sin T = Opposite side of T/Hypotenuse = SU/TU = 12/13

cos T = Adjacent side of T / Hypotenuse = TS/TU = 5/13

tan T = Opposite side of T/Adjacent side of T = SU/TS = 12/5

sin U = Opposite side of U/Hypotenuse = TS/TU = 5/13

cos U = Adjacent side of U / Hypotenuse = SU/TU = 12/13

tan U = Opposite side of U/Adjacent side of U = TS/SU = 5/12

3. In right angled YXZ, X = 90°, XZ = 8 cm, YZ = 17 cm, find sin Y, cos Y, tan Y, sin Z, cos Z, tan Z.

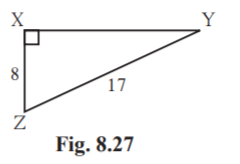
Solution:

Given X = 90°

XZ = 8 cm

YZ = 17 cm

YZ² = XZ² +XY² [Pythagoras theorem]

17² = 8² +XY²

XY² = 17² -8²

XY² = 289-64

XY² = 225

Taking square root on both sides

XY = 15

sin Y = Opposite side of Y/Hypotenuse = XZ/YZ = 8/17

cos Y = Adjacent side of Y / Hypotenuse = XY/YZ = 15/17

tan Y = Opposite side of Y/Adjacent side of Y = XZ/XY = 8/15

sin Z = Opposite side of Z/Hypotenuse = XY/YZ = 15/17

cos Z = Adjacent side of Z/ Hypotenuse = XZ/YZ = 8/17

tan Z = Opposite side of Z/Adjacent side of Z = XY/XZ = 15/8

4. In right angled LMN, if N = , M = 90°, cos = 24/ 25 , find sin and tan Similarly, find (sin² ) and (cos² )

Maharashtra Board Sol Class 9 Maths p2 chapter 8-8

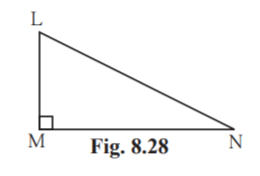
Solution:

Given N =

M = 90°

cos = 24/25

cos² = (24/25)² = 576/625

sin² +cos² = 1

sin² +(24/25)² = 1

sin² = 1-(24/25)²

sin² = 1-(576/625)

sin² = (625-576)/625

sin² = 49/625

Taking square root on both sides

sin = 7/25

tan = sin /cos

tan = (7/25) ÷ (24/25)

tan = (7/25) × (25/24)

tan = 7/24

Hence sin = 7/25

tan = 7/24

sin² = 49/625

cos² = (24/25)² = 576/625

5. Fill in the blanks.

(i) sin20° = cos ___˚

(ii) tan30°× tan ___° =1

(iii) cos40° = sin ___°

Solution:

(i) sin = cos (90-)

sin 20˚= cos (90-20) = cos 70˚

Hence, sin 20˚= cos 70˚

(ii)tan ×tan (90-) = 1

tan 30˚×tan (90-30) = 1

tan 30˚×tan (60)˚ = 1

Hence tan 30˚×tan 60˚ = 1

(iii) cos = sin (90-)

cos 40˚ = sin (90-40)˚

cos 40˚ = sin 50˚

Hence, cos 40˚ = sin 50˚