The Class 8 is an important year in a student’s life and Maharashtra State Board Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 8 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 8 Maths Book syllabus.
Practice Set 13.1 Page No: 85
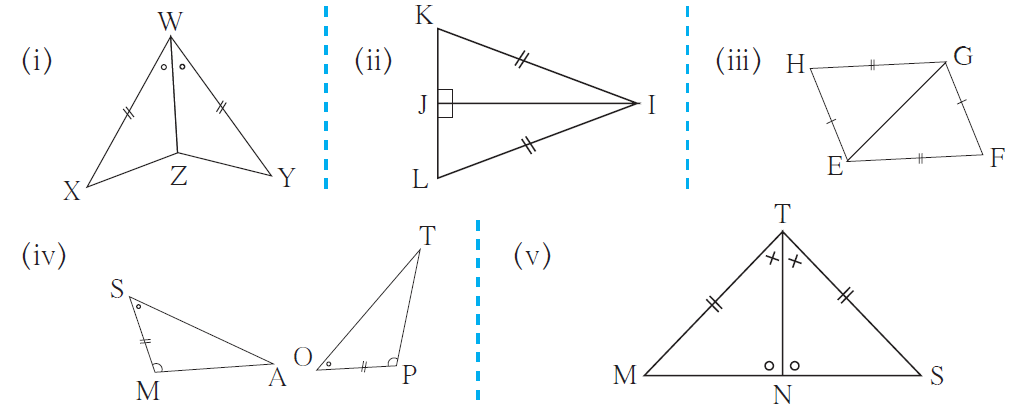
1. In each pair of triangles in the following figures, parts bearing identical marks are congruent. State the test and correspondence of vertices by which triangles in each pair are congruent.
Solution:
(i) By SAS test, in the correspondence XWZ ↔ YWZ.
(ii) By Hypotenuse-side test, in the correspondence KJI ↔ LJI.
(iii) By SSS test, in the correspondence HEG ↔ FGE.
(iv) By ASA test, in the correspondence SMA ↔ OPT.
(v) By SAA test, in the correspondence MTN ↔ STN.
Practice Set 13.2 Page No: 87
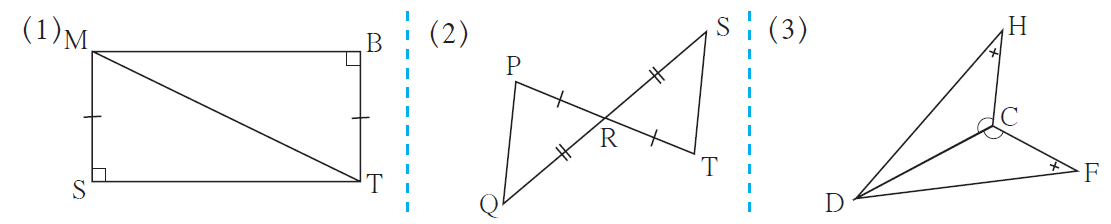
1. In each pair of triangles given below, parts shown by identical marks are congruent. State the test and the one to one correspondence of vertices by which triangles in each pair are congruent and remaining congruent parts.
Solution:
(1)
In ∆MST and ∆TBM, we have
side MS ≅ side TB …. (given)
∠MST ≅ ∠TBM …. (right angle)
And, side MT is common
Hence, by Hypotenuse-side test ∆MST ≅ ∆TBM.
Now, from corresponding parts of congruent triangles
side ST ≅ side MB,
∠SMT ≅ ∠BTM,
∠STM ≅ ∠BMT.
(2)
In ∆PRQ and ∆TRS, we have
side PR ≅ side RT …. (given)
side QR ≅ side RS …. (given)
∠PRQ ≅ ∠SRT …. (vertically opposite angles)
Hence, by SAS test ∆PRQ ≅ ∆TRS.
Now, from corresponding parts of congruent triangles
side PQ ≅ side ST,
∠QPR ≅ ∠STR,
∠PQR ≅ ∠TSR.
(3)
In ∆DHC and ∆DFC, we have
∠DCH ≅ ∠DCF …. (given)
∠DHC ≅ ∠DFC …. (given)
And, side DC is common
Hence, by AAS test ∆DHC ≅ ∆DFC.
Now, from corresponding parts of congruent triangles
side DH ≅ side DF,
side HC ≅ side FC,
∠HDC ≅ ∠FDC.
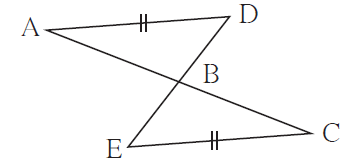
2. In the adjacent figure, seg AD ≅ seg EC. Which additional information is needed to show that ΔABD and ΔEBC will be congruent by A-A-S test?
Solution:
In ∆ABD and ∆EBC, we have
side AD ≅ side EC … (given)
∠ABD ≅ ∠EBC … (vertically opposite angles)
Now,
In order to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test, one of the following is required:
∠BAD ≅ ∠BCE
or
∠BDA ≅ ∠BEC.