Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
The Class 8 is an important year in a student’s life and Maharashtra State Board Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 8 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 8 Maths Book syllabus.

Practice Set 12.1 Page No: 77
1. Each equation is followed by the values of the variable. Decide whether
these values are the solutions of that equation.
(1) x –4 = 3, x = -1, 7, -7 (2) 9m = 81, m = 3, 9, -3
(3) 2a + 4 = 0, a = 2, -2, 1 (4) 3 –y = 4, y = -1, 1, 2
Solution:
(1) Given equation: x –4 = 3 … (i)
Firstly, putting x = -1 in (i) we have
(-1) – 4 = 3
⇒ -5 ≠ 3
Thus, x = -1 is not a solution of the given equation.
Secondly, putting x = 7 in (i) we have
(7) – 4 = 3
⇒ 3 = 3
Thus, x = 7 is the solution of the given equation.
Lastly, putting x = -7 in (i) we have
(-7) – 4 = 3
⇒ -11 ≠ 3
Thus, x = -7 is not a solution of the given equation.
(2) Given equation: 9m = 81… (i)
Firstly, putting m = 3 in (i) we have
9(3) = 81
⇒ 27 ≠ 81
Thus, m = 3 is not a solution of the given equation.
Secondly, putting m = 9 in (i) we have
9(9) = 81
⇒ 81 = 81
Thus, m = 9 is the solution of the given equation.
Lastly, putting m = -3 in (i) we have
9(-3) = 81
⇒ -27 ≠ 81
Thus, m = -3 is not a solution of the given equation.
(3) Given equation: 2a + 4 = 0… (i)
Firstly, putting a = 2 in (i) we have
2(2) + 4 = 0
4 + 4 = 0
⇒ 8 ≠ 0
Thus, a = 2 is not a solution of the given equation.
Secondly, putting a = -2 in (i) we have
2(-2) + 4 = 0
-4 + 4 = 0
⇒ 0 = 0
Thus, a = -2 is the solution of the given equation.
Lastly, putting a = 1 in (i) we have
2(1) + 4 = 0
2 + 4 = 0
⇒ 6 ≠ 0
Thus, a = 1 is not a solution of the given equation.
(4) Given equation: 3 –y = 4 … (i)
Firstly, putting y = -1 in (i) we have
3 – (-1) = 4
3 + 1 = 4
⇒ 4 = 4
Thus, y = -1 is not a solution of the given equation.
Secondly, putting y = 1 in (i) we have
3 – (1) = 4
⇒ 2 ≠ 4
Thus, y = 1 is the solution of the given equation.
Lastly, putting y = 2 in (i) we have
3 – (2) = 4
⇒ 1 ≠ 4
Thus, y = 2 is not a solution of the given equation.
2. Solve the following equations.
(1) 17p –2 = 49
(2) 2m + 7 = 9
(3) 3x + 12 = 2x –4
(4) 5(x –3) = 3(x + 2)
(5) 9/8x + 1 = 10
(6) y/7 + (y –4)/3 = 2
(7) 13x – 5 = 3/2
(8) 3(y + 8) = 10(y –4) + 8
(10) (y – 4)/ 3 + 3y = 4
(11)
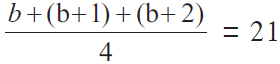
Solution:
(1) Given equation,
17p –2 = 49
Adding 2 on both the sides, we have
17p – 2 + 2 = 49 + 2
17p = 51
Now, dividing by 17 on both the sides, we have
17p/17 = 51/17
p = 3
Thus, p = 3 is the solution of the given equation.
(2) Given equation,
2m + 7 = 9
Subtracting 7 from both the sides, we have
2m + 7 – 7 = 9 – 7
2m = 2
Now, dividing by 2 on both sides, we have
2m/2 = 2/2
m = 1
Thus, m = 1 is the solution of the given equation.
(3) Given equation,
3x + 12 = 2x – 4
Subtracting 12 from both the sides, we have
3x + 12 – 12 = 2x – 4 – 12
3x = 2x – 16
Now, subtracting 2x from both the sides, we have
3x – 2x = 2x – 2x – 16
x = -16
Thus, x = -16 is the solution of the equation.
(4) Given equation,
5(x –3) = 3(x + 2)
On removing the brackets, we get
5x – 15 = 3x + 6
Adding 15 to both sides, we have
5x – 15 + 15 = 3x + 6 + 15
5x = 3x + 21
Subtracting 3x from both the sides, we get
5x – 3x = 3x – 3x + 21
2x = -9
Now, dividing by 2 on both sides, we get
2x/(2) = 21/2
x = 21/2
Thus, x = 21/2 is the solution of the equation.
(5) Given equation,
9/8x + 1 = 10
Multiplying by 8 on both the sides, we have
8 x (9/8x + 1) = 10 x 8
9x + 8 = 80
Subtracting 8 from both the sides, we have
9x + 8 – 8 = 80 – 8
9x = 72
Now, dividing by 9 on the sides, we have
9x/9 = 72/9
x = 8
Thus, x = 9 is the solution of the equation.
(6) Given equation,
y/7 + (y –4)/3 = 2
On multiplying both sides by 21, we have
21 x (y/7) + 21 x [(y – 4)/3] = 2 x 21
3y + 7(y –4) = 42
3y + 7y – 28 = 42
10y – 28 = 42
Now, adding 28 on both sides, we have
10y – 28 + 28 = 42 + 28
10y = 70
Lastly, dividing both sides by 10, we have
10y/ 10 = 70/10
y = 7
Thus, y = 7 is the solution of the equation.
(7) Given equation,
13x – 5 = 3/2
Multiplying both sides by 2, we have
2 × (13x –5) = 2 x 3/2
26x – 10 = 3
On adding 10 to both the sides, we have
26x – 10 + 10 = 3 + 10
26x = 13
Now, dividing both sides by 26, we have
26x/ 26 = 13/26
x = ½
Thus, x = ½ is the solution of the equation.
(8) Given equation,
3(y + 8) = 10(y –4) + 8
On removing the brackets, we have
3y + 24 = 10y – 40 + 8
3y + 24 = 10y – 32
Subtracting 3y on both sides, we have
3y – 3y + 24 = 10y – 32 – 3y
24 = 7y – 32
Now, adding 32 to both sides, we have
24 + 32 = 7y – 32 + 32
56 = 7y
Dividing both sides by 7, we get
7y/7 = 56/7
y = 8
Thus, y = 8 is the solution of the equation.
(9) Given equation,
(x –9)/ (x –5) = 5/7
Multiplying by 7 both the sides, we have
7 x [(x –9)/ (x –5)] = 5/7 x 7
(7x –63)/ (x –5) = 5
Now, multiplying (x –5) to both sides, we have
(x –5) × [(7x –63)/ (x –5)] = 5 × (x –5)
(7x –63) = 5x – 25
Now, adding 63 on both sides, we have
7x – 63 + 63 = 5x – 25 + 63
7x = 5x + 38
Subtracting 5x from both the sides, we have
7x – 5x = 5x – 5x + 38
2x = 38
Lastly, dividing both sides by 2
2x/2 = 38/2
x = 19
Thus, x = 19 is the solution of the equation.
(10) Given equation,
(y – 4)/ 3 + 3y = 4
On multiplying both sides by 3, we have
3 x [(y –4)/ 3] + 3 x 3y = 4 x 3
y – 4 + 9y = 12
10y – 4 = 12
Now, adding 4 to both sides, we have
10y –4 + 4 = 12 + 4
10y = 16
Lastly dividing both sides by 10, we have
10y/10 = 16/10
y = 8/5
Thus, y = 8/5 is the solution of the equation.
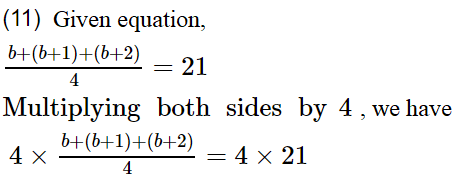
b + (b + 1) + (b + 2) = 84
3b + 3 = 84
Subtracting 3 from both the sides, we have
3b + 3 – 3 = 84 – 3
3b = 81
Now, dividing by 3 both sides, we get
3b/3 = 81/3
b = 27
Thus, b = 27 is the solution of the equation.
Practice Set 12.2 Page No: 77
1. Mother is 25 year older than her son. Find son’s age if after 8 years ratio of son’s age to mother’s age will be 4/9.
Solution:
Let’s consider the present age of the son be x years.
Then, the age of the mother = (x + 25) years
Now, after 8 years
Age of son = (x + 8) years
Age of mother = (x + 25+ 8) years = (x + 33) years
From the given information, we have
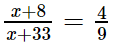
On cross-multiplying,
9(x + 8) = 4(x + 33)
9x + 72 = 4x + 132
9x – 4x = 132 – 72
5x = 60
⇒ x = 12
Thus, the present age of the son is 12 years.
2. The denominator of a fraction is greater than its numerator by 12. If the numerator is decreased by 2 and the denominator is increased by 7, the new fraction is equivalent with 1/2. Find the fraction.
Solution:
Let’s assume the numerator of the fraction to be x.
So,
Denominator = x + 12
The factor = x/(x + 12)
Now, from the given information we have
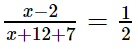
On cross multiplying,
2 (x –2) = (x + 12 + 7)
2x – 4 = x + 19
2x – x = 19 + 4
x = 23
Hence, the numerator of the fraction is 23 and the denominator of the fraction is (23 + 12) = 35.
Therefore, the fraction is 23/35.
3. The ratio of weights of copper and zinc in brass is 13:7. Find the weight of zinc in a brass utensil weighing 700 gm.
Solution:
Given that the ratio of weights of copper and zinc in brass is 13: 7.
So, let the weight of the copper in brass be 13x
And the weight of zinc in brass be 7x
Now, from the given information we have
Weight of brass = 700 gm
⇒ Weight of copper in brass + weight of zinc in brass = 700 gm
13x + 7x = 700
20x = 700
x = 700/20
x = 35
Therefore, the wight of zinc in brass = 7 x 35 = 245 gm.
4. Find three consecutive whole numbers whose sum is more than 45 but less than 54.
Solution:
Let’s take the three consecutive whole numbers to be x, x + 1 and x + 2.
The given conditions are,
45 <x + (x + 1) + (x + 2) and x + (x + 1) + (x + 2) <54
45 <3x + 3 and 3x + 3 <54
45 – 3 <3x and 3x <54 – 3
42 <3x and 3x <51
14 <x and x <17
So, x = 15, 16
Now, if x = 15
The other numbers are 16, 17.
If x = 16,
The other number are 17, 18.
Therefore, the three consecutive whole number are 15, 16, 17 or 16, 17, 18.
5. In a two-digit number, digit at the ten’s place is twice the digit at unit’s place. If the number obtained by interchanging the digits is added to the original number, the sum is 66. Find the number.
Solution:
Let’s assume the digit at the unit’s place to be x.
Digital at tens place = 2x
Original number = 2x × 10 + x = 21x
Now, the number obtained by interchanged the digits = x × 10 + 2x = 12x
From the given information,
12x + 21x = 66
33x = 66
⇒ x = 2
So, the unit’s digit = 2 and the ten’s digit = 2 x 2 = 4
Therefore, the number is 42.
6. Some tickets of Rs 200 and some of Rs 100, of a drama in a theatre were sold. The number of tickets of Rs 200 sold was 20 more than the number of tickets of Rs 100. The total amount received by the theatre by sale of tickets was Rs 37000. Find the number of Rs 100 tickets sold.
Solution:
Let’s consider the number of tickets of Rs 100 be x.
Then, the number of tickets of Rs 200 = x + 20
From the given information,
100 (x) + 200 (x + 20) = 37000
100x + 200x + 4000 = 37000
300x = 37000 – 400
300x = 33000
⇒ x = 110
The number of tickets of Rs 100 = 110.
And, the number of tickets of Rs 200 = 110 + 20 = 130.
Therefore, the number of tickets of Rs 100 is 110.
7. Of the three consecutive natural numbers, five times the smallest number is 9 more than four times the greatest number, find the numbers.
Solution:
Let’s consider the three consecutive natural numbers to be x, x + 1 and x + 2.
From the given information,
5 (x) = 4 (x + 2) + 9
5x = 4x + 8 + 9
5x – 4x = 17
⇒ x = 17
So, the three consecutive natural number are 17, 17 + 1 and 17 + 2.
Therefore, the three consecutive natural number are 17, 18 and 19.
8. Raju sold a bicycle to Amit at 8% profit. Amit repaired it spending Rs 54. Then he sold the bicycle to Nikhil for Rs 1134 with no loss and no profit. Find the cost price of the bicycle for which Raju purchased it.
Solution:
Let’s assume the cost price of the bicycle for which Raju purchased it be x.
And the selling of the bicycle = 108% of cost price
= 108/100 × x
Also given, Amit repaired the cycle spending Rs 54.
So,
The cost price of the bicycle for which Nikhil purchased = (108/100)x + 54
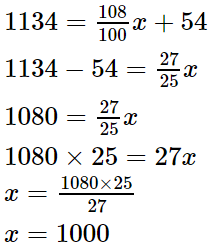
x = (1080 x 25)/ 27
x = 1000
Therefore, the cost price of the bicycle for which Raju purchased it is Rs 1000.
9. A Cricket player scored 180 runs in the first match and 257 runs in the second match. Find the number of runs he should score in the third match so that the average of runs in the three matches be 230.
Solution:
Given,
Runs scored in the first match = 180
Runs scored is the second match = 257
So,
The total run scored in all three matches = Average x Number of matches
= 230 x 3
= 690
Now,
Run scored in third match = 690 – (180 + 257)
= 690 – 437
= 253
Therefore, the runs he should score in the third match is 253.
10. Sudhir’s present age is 5 more than three times the age of Viru. Anil’s age is half the age of Sudhir. If the ratio of the sum of Sudhir’s and Viru’s age to three times Anil’s age is 5:6, then find Viru’s age.
Solution:
Let’s take Viru’s present age to be ‘x’ years.
Now, Sudhir’s present age = (5 + 3x) years
Anil’s present age = (5 + 3x)/ 3 years
From the given information,

6 (10 + 8x) = 5 (15 + 9x)
60 + 48x = 75 + 45x
48x – 45x = 75 – 60
3x = 15
x = 5
Therefore, Viru’s age is 5 years.
The value of the variable, which satisfies the given equation is called the solution of the equation. This chapter deals with equations in one variable only. Solving an equation means to find the solution of the equation. The equation obtained by performing the same operation on both sides does not change its solution. Using this property, we obtain new but simpler equations and solve the given equation.