The Class 8 is an important year in a student’s life and Maharashtra State Board Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 8 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 8 Maths Book syllabus.
Practice Set 10.1 Page No: 64
1. Divide. Write the quotient and the remainder.
(1) 21m² ÷ 7m
Solution:
Thus, quotient = 3m and remainder = 0.
(2) 40a³ ÷ (-10a)
Solution:
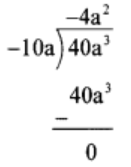
Thus, quotient = -4a2 and remainder = 0.
(3) (- 48p4
) ÷ (- 9p2
)
Solution:
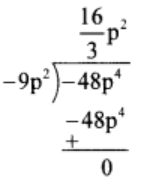
Thus, quotient = 16/3 p2 and remainder = 0.
(4) 40m5
÷ 30m3
Solution:
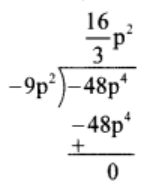
Thus, quotient = 16/3 p2 and remainder = 0.
(5) (5x3
– 3x2
) ÷ x²
Solution:
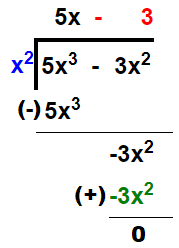
Thus, quotient = 5x – 3 and remainder = 0.
(6) (8p3
– 4p2
) ÷ 2p2
Solution:
Thus, quotient = 4p – 2 and remainder = 0.
(7) (2y3
+ 4y2
+ 3) ÷ 2y2
Solution:
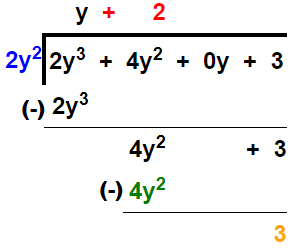
Thus, quotient = y + 2 and remainder = 3.
(8) (21x4
– 14x2
+ 7x) ÷ 7x3
Solution:
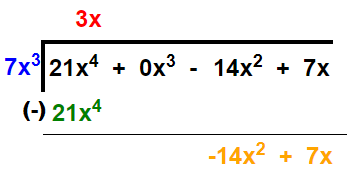
Thus, quotient = 3x and remainder = -14x2 + 7x.
(9) (6x5
– 4x4
+ 8x3
+ 2x2
) ÷ 2x2
Solution:
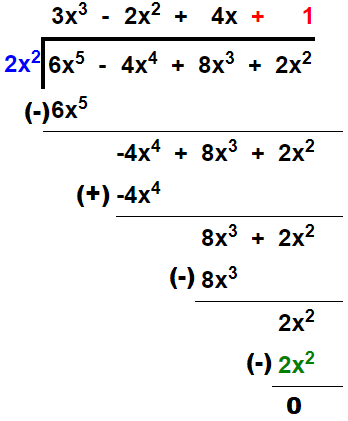
Thus, quotient = 3x3 – 2x2 + 4x + 1 and remainder = 0.
(10) (25m4 – 15m3 + 10m + 8) ÷ 5m3
Solution:
Thus, quotient = 5m – 3 and remainder = 10m + 8.
Practice Set 10.2 Page No: 66
1. Divide and write the quotient and the remainder.
(1) (y2 + 10y + 24) ÷ (y + 4)
Solution:
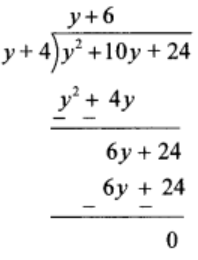
Thus, quotient = y + 6 and remainder = 0
(2) (p2 + 7p – 5) ÷ (p + 3)
Solution:
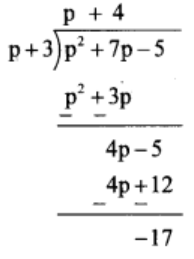
Thus, quotient = p + 4 and remainder = -17
(3) (3x + 2x2 + 4x3 ) ÷ (x – 4)
Solution:
Writing the dividend in descending order of their indices, we have
3x + 2x² + 4x³ = 4x³ + 2x² + 3x
Thus, quotient = 4x2 + 18x + 75 and remainder = 300
(4) (2m3 + m2 + m + 9) ÷ (2m – 1)
Solution:
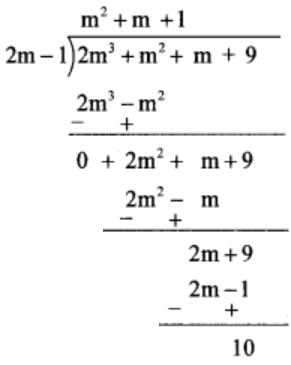
Thus, quotient = m2 + m + 1 and remainder = 10
(5) (3x – 3x2 – 12 + x4 + x3 ) ÷ (2 + x2 )
Solution:
Writing the dividend in descending order of their indices, we have
(x4 + x3 – 3x2 + 3x – 12) ÷ (x2 + 2)
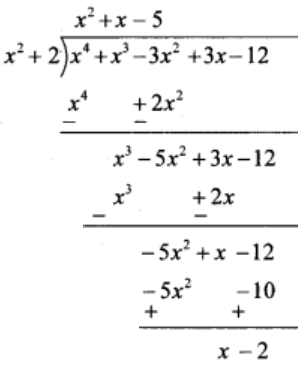
Thus, quotient = x2 + x – 5 and remainder = x – 2.
(6) (a4 – a3 + a2 – a + 1) ÷ (a3 – 2)
Solution:
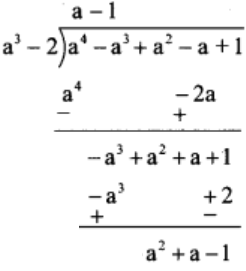
Thus, quotient = a – 1 and remainder = a2 + a – 1.
(7) (4x4 – 5x3 – 7x + 1) ÷ (4x – 1)
Solution:
Writing the dividend in descending order of their indices, we have
(4x4 – 5x3 – 7x + 1) = (4x4 – 5x3 + 0x2 – 7x + 1)
Thus, quotient = x3 – x2 – x/4 – 29/16 and remainder = -13/16.